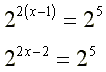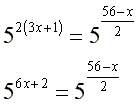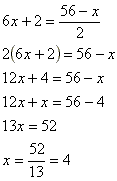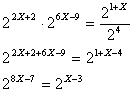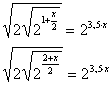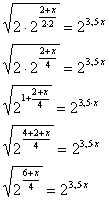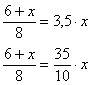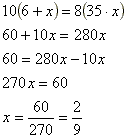Equações exponenciais

Matematica | Vestibular

Site oficial do Prof. Caju

aula particular matemática rio de janeiro

Início

| Fale Conosco

| Ajuda

Para iniciar este estudo, você deve ter lido a matéria "Aritmética Básica". Pois lá você aprende os fundamentos utilizados nesta matéria (propriedades de potenciação e radiciação).

Para termos uma equação igualdade ou seja, alguma coisa igualada à outra. devemos ter uma

E para ser equação exponencial devemos ter uma igualdade que tenha uma variável (normalmente X) colocada no expoente (potência). Para resolvê-las utilizamos métodos que se valem das propriedades que acabamos de estudar.

Não existe uma fórmula mágica para resolução de equações exponenciais, existe um objetivo a ser alcançado. Quando nos deparamos com uma equação exponencial devemos procurar um método de IGUALAR AS BASES de ambos os lados da igualdade. Isso mesmo, o objetivo é esse IGUALAR AS BASES. Veja abaixo vários exemplos resolvidos.

	Esta é a nossa equação exponencial. Temos uma igualdade e veja que sua variável (X) está como expoente do termo à esquerda desta igualdade. Bom, o nosso objetivo é igualar as bases, vamos fatorar ambos os lados:
	O lado esquerdo já estava fatorado. Agora temos os dois lados com a mesma base. Chegamos ao objetivo. Agora devemos "CORTAR" as bases de ambos os lados.
	Pronto, com as bases "cortadas" mantemos os expoentes e calculamos uma equação do primeiro grau.
x=2	Esta é a solução!!

Vejam agora um exemplo um pouquinho mais difícil:

	O nosso objetivo é sempre o mesmo, igualar as bases. Vamos fatorar ambos os lados.
	Temos agora que utilizar as propriedade de potenciação
	Pronto, estamos com as bases iguais. Vamos cortar e resolver a equação do primeiro grau novamente.
2x-2=5	Aplicando as propriedades operatórias.
2x=5+2 2x=7 x=7/2	Esta é a solução

Vamos aumentar mais uma vez o nível.

	Novamente começamos fatorando.
	Para igualar as bases, vamos aplicar as propriedades de potenciação e radiciação.
	Com as bases iguais vamos operar os expoentes
	Esta é a nossa solução x=4

Mais um exemplo um pouco mais difícil.

	Este exemplo é um pouco mais difícil pois tem um expoento no expoente. Note que teremos que igualar as bases duas vezes. Preste atenção. Vamos fatorar
	Agora podemos cortar as bases. Sobram os expoentes.
	Temos outra equação exponencial. Novamente vamos fatorar e igualar as bases.
	Corta-se as bases.
x+1=2 x=2-1 x=1	Esta é a nossa solução, x=1

Novamente vamos aumentar a dificuldade:

	Como sempre, vamos fatorar.
	Vamos aplicar as propriedades operatórias de potenciação para multiplicação e divisão de mesma base.
	Pronto, objetivo alcançado. Cortando...
8x-7=x-3 8x-x=7-3 7x=4 x=4/7	Esta é a solução

Agora com mais raízes.

	Esta parece ser bem mais difícil, né?? Mas a dificuldade é a mesma, você precisa ter os mesmo conhecimentos para resolve-la. As bases já estão definidas, vai ser 2. O que devemos fazer é transformar o lado esquerdo em uma única raiz usando as propriedades de radiciação. Vamos primeiro trabalhar no 2 mais de dentro.
	Agora é só fazer a multiplicação de potências de mesma base.
	Uma raiz já foi. Vamos fazer a mesma coisa com as outras.
	Mais uma vez para matar a última raiz.
	Bases iguais, corta-las...
	Agora é só operar e isolar "x".
	Esta é a nossa solução.

Veja uma que precisa de Bhaskara para resolver:

	Precisamos igualar as bases mas nenhum dos lados da igualdade pode ser fatorado. Iremos usar uma propriedade que aprendemos na lição passada: qualquer número elevado na potência zero vale 1 (X^o=1). Então o lado direito da igualdade pode ser 3^o.
	Agora com as bases igualadas vamos corta-las.
x²-x-6=0	Agora é uma equação do segundo grau. Aplicando Bhaskara achamos suas raízes.
{-2 e 3}	Esta é a solução, "x" pode ser qualquer um destes valores.

Última agora

3·2^x+3=192	A única diferença deste exemplo é que antes de fatorar para tentar igualar as bases temos que "passar" o três que está multiplicando para o lado direito dividindo.
2^x+3=192/3	Efetuando o cálculo
2^x+3=64	Agora sim!!! Fatoramos para igualar as bases.
2^x+3=2⁶	Cortando...
x+3=6 x=6-3 x=3	Esta é a nossa solução.

Faça agora alguns exercícios que utilizam este mesmo método para resolução. Após isso veja mais exemplos resolvidos com outros métodos de resolução.

equação continuação 2

continuação 3

continuação 4

continuação 5

Currently 3.05/5
1
2
3
4
5

Rating: 3.0/5 (141 votos)

ONLINE

Partilhe esta Página

Matematica | Vestibular

1 • Equações Exponenciais I 2 • Exercícios de Resolução I 3 • Equações Exponenciais II 4 • Exercícios de Resolução II 5 • Função Exp. GRÁFICOS 6 • Inequações Exponenciais 7 • Exercícios

1 • Equações Exponenciais I
2 • Exercícios de Resolução I
3 • Equações Exponenciais II
4 • Exercícios de Resolução II
5 • Função Exp. GRÁFICOS
6 • Inequações Exponenciais
7 • Exercícios